null - 程序员宅基地

如何理解最小二乘法？-程序员宅基地

最小平方法是十九世纪统计学的主题曲。从许多方面来看, 它之于统计学就相当于十八世纪的微积分之于数学。
----乔治·斯蒂格勒的《The History of Statistics》

1 日用而不知

来看一个生活中的例子。比如说，有五把尺子：

用它们来分别测量一线段的长度，得到的数值分别为（颜色指不同的尺子）：

$\begin{array}{c|c} \qquad\qquad&\qquad长度\qquad\\\hline \color{red}红& 10.2 \\\hline \color{blue}蓝& 10.3 \\\hline \color{orange}橙&9.8\\\hline \color{Goldenrod}黄&9.9\\\hline \color{green}绿&9.8\\\end{array}$

之所以出现不同的值可能因为：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

总之就是有误差，这种情况下，一般取平均值来作为线段的长度：

$\overline{x}=\frac{10.2+10.3+9.8+9.9+9.8}{5}=10$

日常中就是这么使用的。可是作为很事'er的数学爱好者，自然要想下：

这样做有道理吗？
用调和平均数行不行？
用中位数行不行？
用几何平均数行不行？

2 最小二乘法

换一种思路来思考刚才的问题。

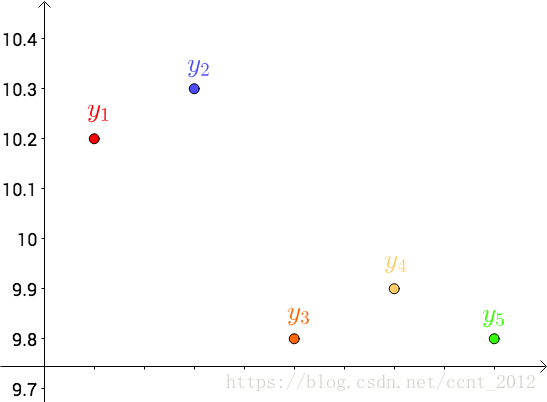
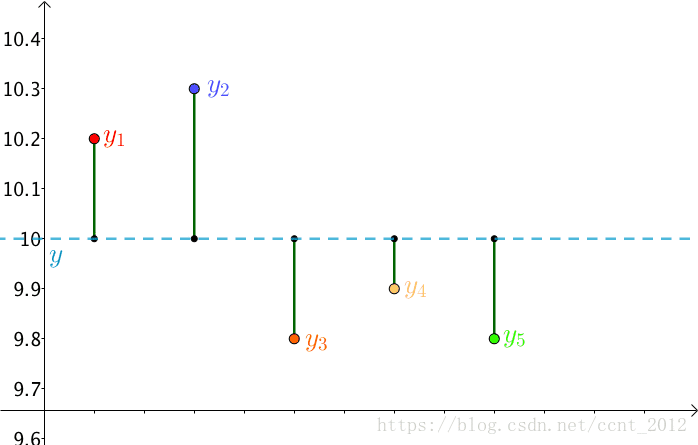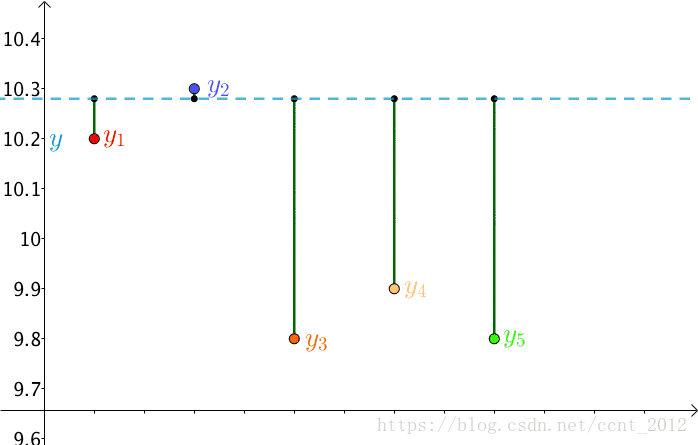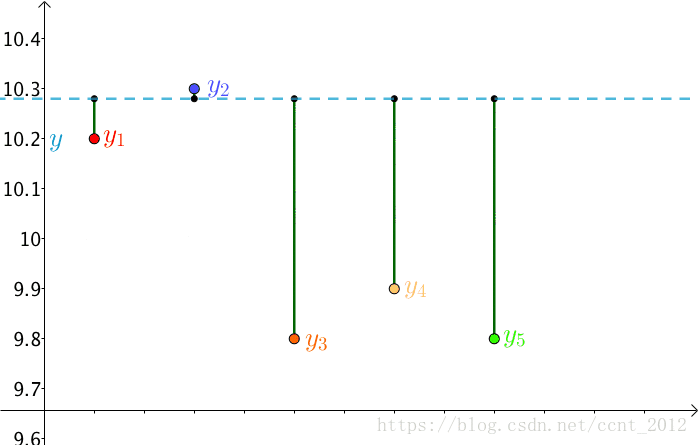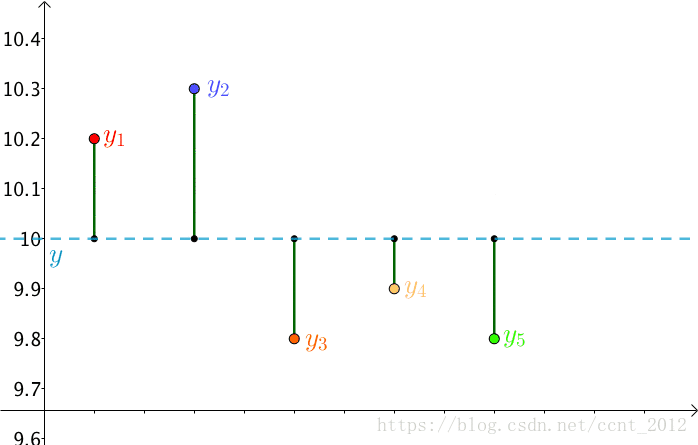
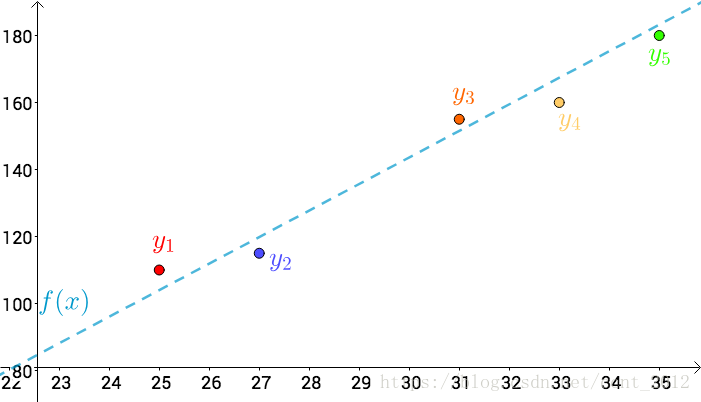
首先，把测试得到的值画在笛卡尔坐标系中，分别记作 $y_i$ ：

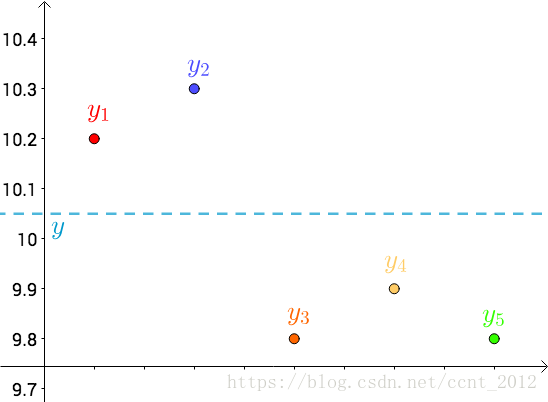
其次，把要猜测的线段长度的真实值用平行于横轴的直线来表示（因为是猜测的，所以用虚线来画），记作 $y$ ：

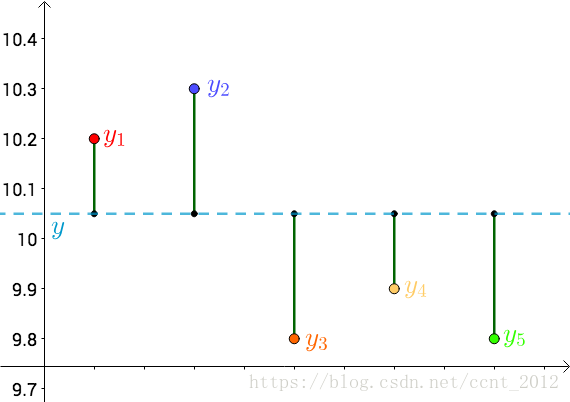
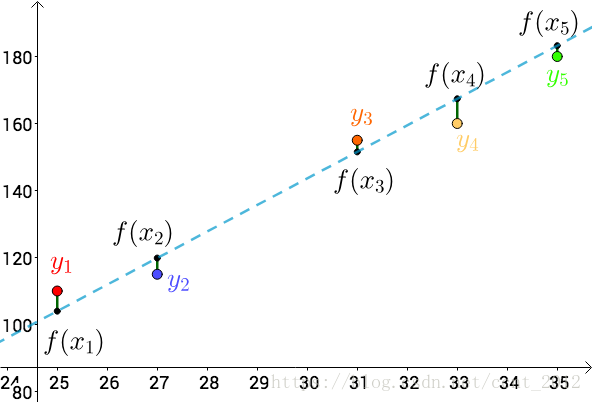
每个点都向 $y$ 做垂线，垂线的长度就是 $|y-y_i|$ ，也可以理解为测量值和真实值之间的误差：

因为误差是长度，还要取绝对值，计算起来麻烦，就干脆用平方来代表误差：

$|y-y_i|\to (y-y_i)^2$

总的误差的平方就是：

$\epsilon=\sum (y-y_i)^2$

因为 $y$ 是猜测的，所以可以不断变换：

自然，总的误差 $\epsilon$ 也是在不断变化的。

法国数学家，阿德里安-馬里·勒讓德（1752－1833，这个头像有点抽象）提出让总的误差的平方最小的 $y$ 就是真值，这是基于，如果误差是随机的，应该围绕真值上下波动（关于这点可以看下“如何理解无偏估计？”）。

这就是最小二乘法，即：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

这个猜想也蛮符合直觉的，来算一下。

这是一个二次函数，对其求导，导数为0的时候取得最小值：

$\begin{aligned} \frac{d}{dy}\epsilon &=\frac{d}{dy}\sum (y-y_i)^2=2\sum (y-y_i)\\ \quad\\ &=2((y-y_1)+(y-y_2)+(y-y_3)+(y-y_4)+(y-y_5))=0 \quad\\\end{aligned}$

进而：

$5y=y_1+y_2+y_3+y_4+y_5\implies y=\frac{y_1+y_2+y_3+y_4+y_5}{5}$

正好是算术平均数。

原来算术平均数可以让误差最小啊，这下看来选用它显得讲道理了。

以下这种方法：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

就是最小二乘法，所谓“二乘”就是平方的意思，台湾直接翻译为最小平方法。

3 推广

算术平均数只是最小二乘法的特例，适用范围比较狭窄。而最小二乘法用途就广泛。

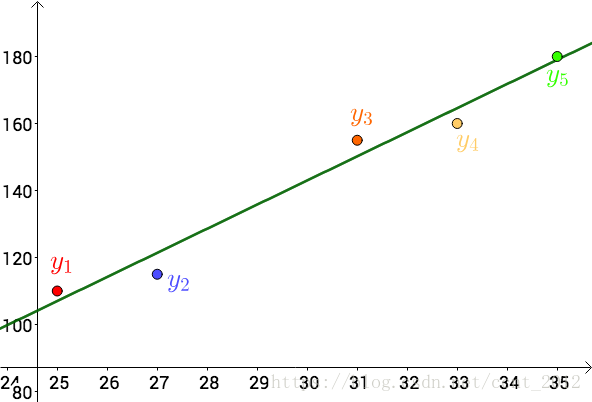
比如温度与冰淇淋的销量：

$\begin{array}{c|c} \qquad\qquad&\qquad销量\qquad\\\hline \color{red}{25^\circ}& 110 \\\hline \color{blue}{27^\circ}& 115 \\\hline \color{orange}{31^\circ}&155\\\hline \color{Goldenrod}{33^\circ}&160\\\hline \color{green}{35^\circ}&180\\\end{array}$

看上去像是某种线性关系：

可以假设这种线性关系为：

$f(x)=ax+b$

通过最小二乘法的思想：

上图的 $i,x,y$ 分别为：

$\begin{array}{c|c|c} \qquad i\qquad&\qquad x\qquad&\qquad y\qquad\\\hline 1&25& 110 \\\hline 2&27& 115 \\\hline 3&31&155\\\hline 4&33&160\\\hline 5&35&180\\\end{array}$

总误差的平方为：

$\epsilon=\sum (f(x_i)-y_i)^2=\sum (ax_i+b-y_i)^2$

不同的 $a,b$ 会导致不同的 $\epsilon$ ，根据多元微积分的知识，当：

$\begin{cases} \frac{\partial}{\partial a}\epsilon=2\sum (ax_i+b-y_i)x_i=0\\ \quad\\ \frac{\partial}{\partial b}\epsilon=2\sum (ax_i+b-y_i)=0\end{cases}$

这个时候 $\epsilon$ 取最小值。

对于 $a,b$ 而言，上述方程组为线性方程组，用之前的数据解出来：

$\begin{cases} a\approx 7.2\\ \quad\\ b\approx -73\end{cases}$

也就是这根直线：

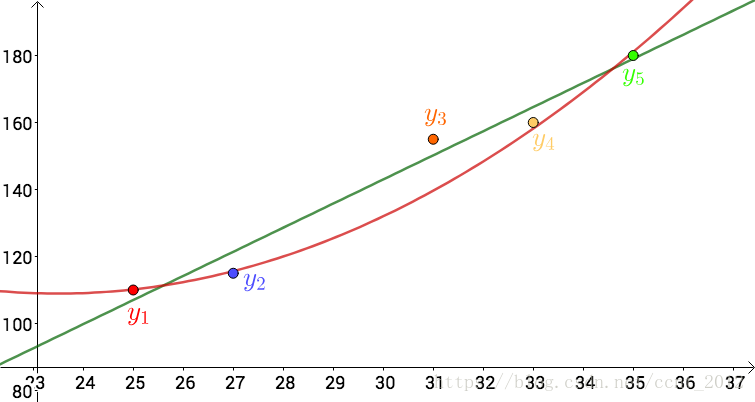
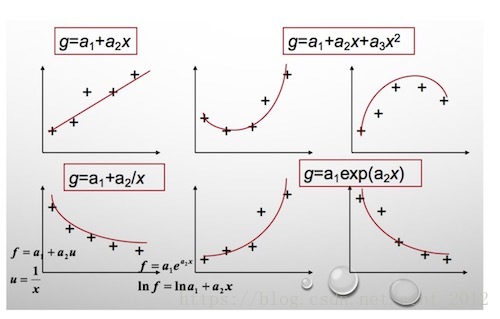
其实，还可以假设：

$f(x)=ax^2+bx+c$

在这个假设下，可以根据最小二乘法，算出 $a,b,c$ ，得到下面这根红色的二次曲线：

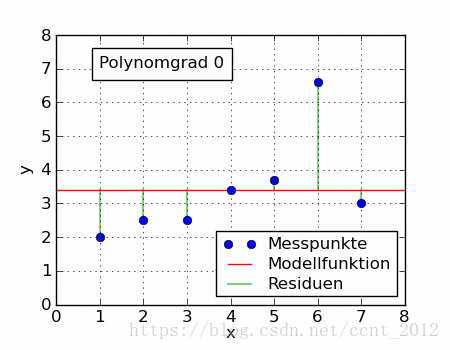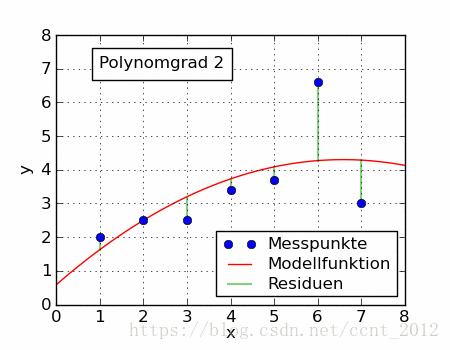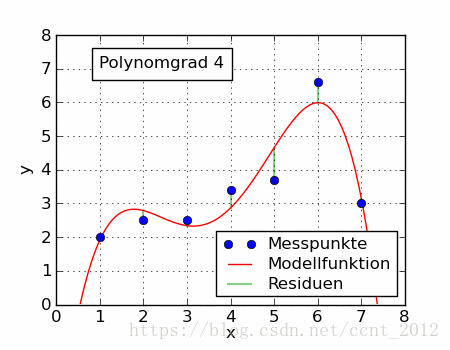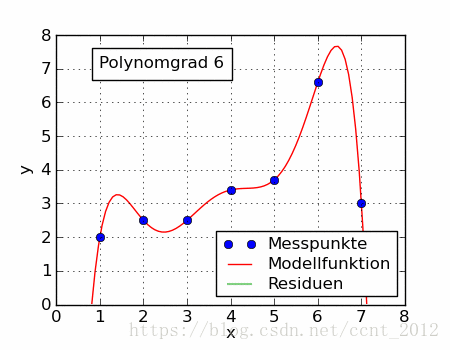
同一组数据，选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线（出处）：

不同的数据，更可以选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线：

$f(x)$ 也不能选择任意的函数，还是有一些讲究的，这里就不介绍了。

4 最小二乘法与正态分布

我们对勒让德的猜测，即最小二乘法，仍然抱有怀疑，万一这个猜测是错误的怎么办？

数学王子高斯（1777－1855）也像我们一样心存怀疑。

高斯换了一个思考框架，通过概率统计那一套来思考。

让我们回到最初测量线段长度的问题。高斯想，通过测量得到了这些值：

每次的测量值 $x_i$ 都和线段长度的真值 $x$ 之间存在一个误差：

$\epsilon_i=x-x_i$

这些误差最终会形成一个概率分布，只是现在不知道误差的概率分布是什么。假设概率密度函数为：

$p(\epsilon)$

再假设一个联合概率密度函数，这样方便把所有的测量数据利用起来：

$\begin{aligned} L(x) &=p(\epsilon_1)p(\epsilon_2)\cdots p(\epsilon_5)\\ \quad\\ &=p(x-x_i)p(x-x_2)\cdots p(x-x_5)\end{aligned}$

讲到这里，有些同学可能已经看出来了上面似然函数了（关于似然函数以及马上要讲到的极大似然估计，可以参考“如何理解极大似然估计法？”）。

因为 $L(x)$ 是关于 $x$ 的函数，并且也是一个概率密度函数（下面分布图形是随便画的）：

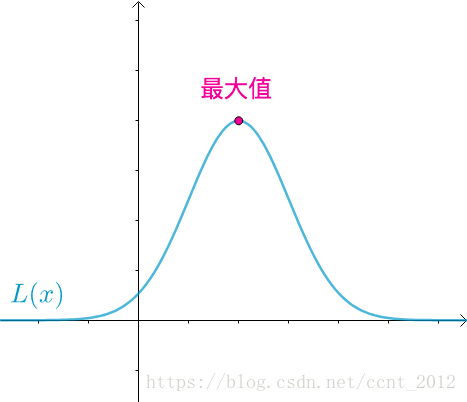
根据极大似然估计的思想，概率最大的最应该出现（既然都出现了，而我又不是“天选之才”，那么自然不会是发生了小概率事件），也就是应该取到下面这点：

当下面这个式子成立时，取得最大值：

$\frac{d}{dx}L(x)=0$

然后高斯想，最小二乘法给出的答案是：

$x=\overline{x}=\frac{x_1+x_2+x_3+x_4+x_5}{5}$

如果最小二乘法是对的，那么 $x=\overline{x}$ 时应该取得最大值，即：

$\frac{d}{dx}L(x)|_{x=\overline{x}}=0$

好，现在可以来解这个微分方程了。最终得到：

$p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

这是什么？这就是正态分布啊。

并且这还是一个充要条件：

$x=\overline{x}\iff p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

也就是说，如果误差的分布是正态分布，那么最小二乘法得到的就是最有可能的值。

那么误差的分布是正态分布吗？

我们相信，误差是由于随机的、无数的、独立的、多个因素造成的，比如之前提到的：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

那么根据中心极限定理（参考“为什么正态分布如此常见？”），误差的分布就应该是正态分布。

因为高斯的努力，才真正奠定了最小二乘法的重要地位。

文章最新版本在（有可能会有后续更新）：如何理解最小二乘法？

本文链接：https://blog.csdn.net/ccnt_2012/article/details/81127117

原作者删帖不实内容删帖广告或垃圾文章投诉

智能推荐

Linux查看登录用户日志_怎么记录linux设备发声的登录和登出-程序员宅基地

文章浏览阅读8.6k次。一、Linux记录用户登录信息文件1　　/var/run/utmp----记录当前正在登录系统的用户信息；2　　/var/log/wtmp----记录当前正在登录和历史登录系统的用户信息；3　　/var/log/btmp：记录失败的登录尝试信息。二、命令用法1.命令last，lastb---show a listing of la_怎么记录linux设备发声的登录和登出

第四章笔记：遍历--算法学中的万能钥匙-程序员宅基地

文章浏览阅读167次。摘要：1. 简介 2. 公园迷宫漫步 3. 无线迷宫与最短（不加权）路径问题 4. 强连通分量1. 简介在计算机科学裡，树的遍历（也称为树的搜索）是圖的遍歷的一种，指的是按照某种规则，不重复地访问某种樹的所有节点的过程。具体的访问操作可能是检查节点的值、更新节点的值等。不同的遍历方式，其访问节点的顺序是不一样的。两种著名的基本遍历策略：深度优先搜索（DFS）和广度优先搜索（B...

【案例分享】使用ActiveReports报表工具，在.NET MVC模式下动态创建报表_activereports.net 实现查询报表功能-程序员宅基地

文章浏览阅读591次。提起报表，大家会觉得即熟悉又陌生，好像常常在工作中使用，又似乎无法准确描述报表。今天我们来一起了解一下什么是报表，报表的结构、构成元素，以及为什么需要报表。什么是报表简单的说：报表就是通过表格、图表等形式来动态显示数据，并为使用者提供浏览、打印、导出和分析的功能，可以用公式表示为：报表 = 多样的布局 + 动态的数据 + 丰富的输出报表通常包含以下组成部分：报表首页：在报表的开..._activereports.net 实现查询报表功能

Ubuntu18.04 + GNOME xrdp + Docker + GUI_docker xrdp ubuntu-程序员宅基地

文章浏览阅读6.6k次。最近实验室需要用Cadence，这个软件的安装非常麻烦，每一次配置都要几个小时，因此打算把Cadence装进Docker。但是Cadence运行时需要GUI，要对Docker进行一些配置。我们实验室的服务器运行的是Ubuntu18.04，默认桌面GNOME，Cadence装进Centos的Docker。安装Ubuntu18.04服务器上安装Ubuntu18.04的教程非常多，在此不赘述了安装..._docker xrdp ubuntu

iOS AVFoundation实现相机功能_ios avcapturestillimageoutput 兼容性 ios17 崩溃-程序员宅基地

文章浏览阅读1.8k次，点赞2次，收藏2次。首先导入头文件#import 导入头文件后创建几个相机必须实现的对象 /** * AVCaptureSession对象来执行输入设备和输出设备之间的数据传递 */ @property (nonatomic, strong) AVCaptureSession* session; /** * 输入设备 */_ios avcapturestillimageoutput 兼容性 ios17 崩溃

Oracle动态性能视图--v$sysstat_oracle v$sysstat视图-程序员宅基地

文章浏览阅读982次。按照OracleDocument中的描述，v$sysstat存储自数据库实例运行那刻起就开始累计全实例(instance-wide)的资源使用情况。类似于v$sesstat，该视图存储下列的统计信息：1>.事件发生次数的统计(如：user commits)2>._oracle v$sysstat视图

随便推点

Vue router报错：NavigationDuplicated {_name: "NavigationDuplicated", name: "NavigationDuplicated"}的解决方法_navigationduplicated {_name: 'navigationduplicated-程序员宅基地

文章浏览阅读7.6k次，点赞2次，收藏9次。我最近做SPA项目开发动态树的时候一直遇到以下错误：当我点击文章管理需要跳转路径时一直报NavigationDuplicated {_name: “NavigationDuplicated”, name: “NavigationDuplicated”}这个错误但是当我点击文章管理后，路径跳转却是成功的<template> <div> 文章管理页面 <..._navigationduplicated {_name: 'navigationduplicated', name: 'navigationduplic

如何理解最小二乘法？-程序员宅基地

智能推荐

Linux查看登录用户日志_怎么记录linux设备发声的登录和登出-程序员宅基地

第四章笔记：遍历--算法学中的万能钥匙-程序员宅基地

【案例分享】使用ActiveReports报表工具，在.NET MVC模式下动态创建报表_activereports.net 实现查询报表功能-程序员宅基地

Ubuntu18.04 + GNOME xrdp + Docker + GUI_docker xrdp ubuntu-程序员宅基地

iOS AVFoundation实现相机功能_ios avcapturestillimageoutput 兼容性 ios17 崩溃-程序员宅基地

Oracle动态性能视图--v$sysstat_oracle v$sysstat视图-程序员宅基地

随便推点

Vue router报错：NavigationDuplicated {_name: "NavigationDuplicated", name: "NavigationDuplicated"}的解决方法_navigationduplicated {_name: 'navigationduplicated-程序员宅基地

Webrtc回声消除模式(Aecm)屏蔽舒适噪音(CNG)_webrtc aecm 杂音-程序员宅基地

医学成像原理与图像处理一：概论_医学成像与图像处理技术知识点总结-程序员宅基地

notepad++ v8.5.3 安装插件，安装失败怎么处理？下载进度为0怎么处理？_nodepa++-程序员宅基地

hive某个字段中包括\n（和换行符冲突）_hive sql \n-程序员宅基地

印象笔记05：如何打造更美的印象笔记超级笔记_好的印象笔记怎么做的-程序员宅基地

推荐文章

热门文章

相关标签