Python数学建模算法与应用（司守奎）--第4章随笔-程序员宅基地

第 4 章线性规划和整数规划模型

4.1 线性规划（Linear Programming，LP）

4.1.1 线性规划模型

线性规划模型的一般形式

$\text{max(or min)}z=c_{1}x_{1}+c_{2}x_{2}+\cdots+c_{n}x_{n}$ ，

$\text{s.t.} \left\{ \begin{matrix} a_{11}x_{1}+a_{12}x_{2}+\cdots+a_{1n}x_{n}\leqslant(or =,\geqslant)b_{1},\hfill \\ a_{21}x_{1}+a_{22}x_{2}+\cdots+a_{2n}x_{n}\leqslant(or =,\geqslant)b_{2},\hfill \\ \cdots\\ a_{m1}x_{1}+a_{m2}x_{2}+\cdots+a_{mn}x_{n}\leqslant(or =,\geqslant)b_{m},\hfill \\ x_{1},x_{2}\cdots,x_{n}\geqslant0 \hfill \end{matrix} \right.$

或简写为

$\text{max}\left(or\ \text{min} \right )z=\sum\limits_{j=1}^{n}c_{j}x_{j},$

$\text{s.t.} \left\{ \begin{matrix} \sum\limits_{j=1}^{n}a_{ij}x_{j}\leqslant\left(or \ =,\geqslant \right )b_{i},i=1,2,\cdots,m,\\ x_{j}\geqslant0,j=1,2,\cdots,n. \hfill \end{matrix} \right.$

其向量表示形式为

$\text{max}\left(or\ \text{min} \right )\textit{\textbf{z}}=\textit{\textbf{c}}^{T}\textit{\textbf{x}}$

$\text{s.t.} \left\{ \begin{matrix} \sum\limits_{j=1}^{n}\textit{\textbf{P}}_{j}x_{j}\leqslant\left(or \ =,\geqslant \right )\textit{\textbf{b}},\\ \textit{\textbf{x}}\geqslant0. \hfill \end{matrix} \right.$

其矩阵表示形式为

$\text{max}\left(or\ \text{min} \right )\textit{\textbf{z}}=\textit{\textbf{c}}^{T}\textit{\textbf{x}}$

$\text{s.t.} \left\{ \begin{matrix} \textit{\textbf{A}}\textit{\textbf{x}}\leqslant\left(or \ =,\geqslant \right )\textit{\textbf{b}},\\ \textit{\textbf{x}}\geqslant0. \hfill \end{matrix} \right.$

其中， $\textit{\textbf{c}}=\left[c_{1},c_{2},\cdots,c_{n} \right ]^{T}$ 为目标函数的系数向量，又称为价值向量；

$\textit{\textbf{x}}=\left[x_{1},x_{2},\cdots,x_{n} \right ]^{T}$ 为决策向量；

$\textit{\textbf{A}}=\left(a_{ij} \right )_{m\times n}$ 为约束方程组的系数矩阵；

$\textit{\textbf{P}}_{j}=\left[a_{1j},a_{2j},\cdots,a_{mj} \right ]^{T},j=1,2,\cdots,n$ 为 $\textit{\textbf{A}}$ 的列向量，又称约束方程组的系数向量；

$\textit{\textbf{b}}=\left[b_{1},b_{2},\cdots,b_{m} \right ]^{T}$ 为约束方程组的常数向量。

4.1.2 模型求解及应用

可以使用 Python 的 cvxpy 库，用于求解凸优化问题。http://www.vcxpy.org/

例 4.2 求解线性规划模型

$\text{max}z=70x_{1}+50x_{2}+60x_{3} \\ \text{s.t.}\left\{\begin{matrix} 2x_{1}+4x_{2}+3x_{3}\leqslant150,\\ 3x_{1}+x_{2}+5x_{3}\leqslant160,\hfill\\ 7x_{1}+3x_{2}+5x_{3}\leqslant200,\\ x_{i}\geqslant0,i=1,2,3.\hfill \end{matrix}\right.$

# 程序文件 ex4_2.py
import cvxpy as cp
from numpy import array
c = array([70, 50, 60])                      # 定义目标向量
a = array([[2, 4, 3],[3, 1, 5], [7, 3, 5]])  # 定义约束矩阵
b = array([150, 160, 200])                   # 定义约束条件的右边向量
x = cp.Variable(3, pos=True)                 # 定义 3 个决策变量
obj = cp.Maximize(c@x)                       # 构造目标函数
cons = [a@x<=b]                              # 构造约束条件
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')                 # 求解问题
print('最优解为：', x.value)
print('最优值为：', prob.value)

例 4.3 某部分今后 5 年考虑以下投资项目，已知：

项目A，从第一年到第四年每年年初需投资，并于次年末收回本利 115%。

项目B，从第三年初需投资，到第五年末能回收本利125%，最大投资额不超过4万元。

项目C，第二年初需投资，到第五年末能收回本利140%，最大投资额不超过3万元。

项目D，五年内每年初购买，于当年末归还，利息收益6%。

部门现有资金10万元，试问如何确定这些项目每年投资额，使第五年末本利总额最大？

建立线性规划模型

$\text{max}z=1.15x_{41}+1.40x_{23}+1.25x_{32}+1.06x_{54,} \\ \text{s.t.}\left\{\begin{matrix} x_{11}+x_{14}=100000,\hfill \\ x_{21}+x_{23}+x_{24}=1.06x_{14},\hfill \\ x_{31}+x_{32}+x_{34}=1.15x_{11}+1.06x_{24},\\ x_{41}+x_{44}=1.15x_{21}+1.06x_{34}, \hfill \\ x_{54}=1.15x_{31}+1.06x-{44},\hfill \\ x_{32}\leqslant40000,x_{23}\leqslant30000,\hfill \\ x_{ij}\geqslant0,i=1,2,3,4,5;j=1,2,3,4.\hfill \end{matrix}\right.$

# 程序文件 ex4_3.py
import cvxpy as cp
x = cp.Variable((5, 4), pos=True)
obj = cp.Maximize(1.15*x[3, 0]+1.40*x[1, 2]+1.25*x[2, 1]+1.06*x[4, 3])
cons = [x[0, 0]+x[0, 3] == 100000,
       x[1, 0]+x[1, 2]+x[1, 3] == 1.06*x[0, 3],
       x[2, 0]+x[2, 1]+x[2, 3] == 1.15*x[0, 0]+1.06*x[1, 3],
       x[3, 0]+x[3, 3] == 1.15*x[1, 0]+1.06*x[2, 3],
       x[4, 3] == 1.15*x[2, 0]+1.06*x[3, 3],
       x[2, 1]<=40000,x[1,2]<=30000]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优解为：', x.value)
print('最优值为：', prob.value)

例 4.4 捷运公司在下一年度的 1~4 月拟租用仓库堆放物资。已知各月所需仓库面积如表 4.2 所示，仓库租借费用随合同同期而定，期限越长，折扣越大。合同每月初均可办理，规定租用面积和期限。每次办理可签一份合同，也可签若干份租用面积和期限不同的合同，试确定该公司签订租借合同的最优决策，使所付租借费用最小。

表 4.2 所需仓库面积和租借仓库费用数据
月份	1	2	3	4
所需仓库面积 / 100 $m^{2}$	15	10	20	12
合同租借期限 / 月	1	2	3	4
合同期内的租费 / 元	2800	4500	6000	7300

建立线性规划模型

$\text{min}z=2800\left(x_{11}+x_{21}+x_{31}+x_{41} \right )+4500\left(x_{12}+x_{22}+x_{32} \right )+6000\left(x_{13}+x_{23} \right )+7300x_{14} \\ \text{s.t.} \left\{\begin{matrix} x_{11}+x_{12}+x_{13}+x_{14} \geqslant15,\hfill \\ x_{12}+x_{13}+x_{14}+x_{21}+x_{22}+x_{23}\geqslant10,\\ x_{13}+x_{14}+x_{22}+x_{23}+x_{31}+x_{32}\geqslant10,\\ x_{14}+x_{23}+x_{32}+x_{41}\geqslant12,\hfill \\ x_{ij}\geqslant0,i=1,2,\cdots,4;\ j=1,2,\cdots,4. \end{matrix}\right.$

# 程序文件 ex4_4.py
import cvxpy as cp
x = cp.Variable((4, 4), pos=True)
obj = cp.Minimize(2800*sum(x[:,0])+4500*sum(x[:3,1])+6000*sum(x[:2,2])+7300*x[0,3])
cons = [sum(x[1,:])>=15,
       sum(x[0,1:])+sum(x[2,:3])>=10,
       sum(x[0,2:])+sum(x[1,1:3])+sum(x[2,:2])>=20,
       x[0,3]+x[1,2]+x[2,1]+x[3,0]>=12]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优解为：\n',x.value)
print('最优值为：',prob.value)

例 4.5 计算 6 个产地 8 个销地的最小费用运输问题，单位商品运价如表 4.3 所示

表 4.3 单位商品运价表
	$B_{1}$	$B_{2}$	$B_{3}$	$B_{4}$	$B_{5}$	$B_{6}$	$B_{7}$	$B_{8}$	产量
$A_{1}$	6	4	6	7	4	2	5	9	60
$A_{2}$	4	9	5	3	8	5	8	2	55
$A_{3}$	5	2	1	9	7	4	3	3	51
$A_{4}$	7	6	7	3	9	2	7	1	43
$A_{5}$	2	3	9	5	7	2	6	5	41
$A_{6}$	5	5	2	2	8	1	4	3	52
销量	35	37	22	32	41	32	43	38

建立线性规划模型

$\text{min}\sum\limits_{i=1}^{6}\sum\limits_{j=1}^{8}c_{ij}x_{ij}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{i=1}^{6}x_{ij}=d_{j},\ j=1,2,\cdots,8, \hfill \\ \sum\limits_{j=1}^{8}x_{ij} \leqslant e_{ij}, \ i=1,2,\cdots,6, \hfill \\ x_{ij} \geqslant0,\ i=1,2,\cdots,6; \ j=1,2,\cdots,8. \end{matrix}\right.$

# 程序文件 ex4_5_1.py
import numpy as np
import cvxpy as cp
import pandas as pd
c = np.genfromtxt('data4_5_1.txt', dtype=float, max_rows=6, usecols=range(8)) # 读前 6 行前 8 列数据
e = np.genfromtxt('data4_5_1.txt', dtype=float, max_rows=6, usecols=8)        # 读最后一列数据
d = np.genfromtxt('data4_5_1.txt', dtype=float, skip_header=6)                # 读最后一行数据
x = cp.Variable((6, 8), pos=True)
obj = cp.Minimize(cp.sum(cp.multiply(c, x)))
con = [cp.sum(x,axis=0)==d,
      cp.sum(x,axis=1)<=e]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print('最优解为：\n', x.value)
print('最优值为：', prob.value)
xd = pd.DataFrame(x.value)
xd.to_excel('data4_5_2.xlsx')                                                 # 数据写到 excel 文件，便于做表使用

# 通过 excel 文件传递数据
# 程序文件 ex4_5_2.py
import cvxpy as cp
import pandas as pd
data = pd.read_excel('data4_5_3.xlsx', header=None)
data = data.values
c = data[:-1, :-1]
d = data[-1, :-1]
e = data[:-1, -1]
x = cp.Variable((6, 8), pos=True)
obj = cp.Minimize(cp.sum(cp.multiply(c, x)))
con = [cp.sum(x,axis=0)==d,
      cp.sum(x,axis=1)<=e]
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print('最优解为：\n', x.value)
print('最优值为：', prob.value)
xd = pd.DataFrame(x.value)
xd.to_excel('data4_5_4.xlsx')

4.2 整数规划（Integer Programming，IP）

4.2.1 整数线性规划模型

从决策变量的取值范围，可分为

（1）纯整数规划

（2）混合整数规划：决策变量一部分必须取整，另一部分可以不取整

（3）0-1整数规划：决策变量智能取 0 或 1。

$\text{max}\left(or \ \text{min} \right )z=\sum\limits_{j=1}^{n}c_{j}x_{j}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{j=1}^{n}a_{ij}x_{j} \leqslant \left(or\ =,\geqslant \right)b_{i},\ i=1,2,\cdots,m, \\ x_{j} \geqslant0, \ j=1,2,\cdots,n, \hfill \\ x_{1},x_{2},\cdots,x_{n} \ \mbox{partial or full integer} . \hfill \end{matrix} \right.$

例 4.6 背包问题

一个旅行者外出旅行，携带一背包，装一些最有用的东西，共有 $n$ 件物品供选择。已知每件物品的“使用价值” $c_{j}$ 和重量 $a_{j}$ ，要求

（1）最多携带物品的质量为 $b\ \text{kg}$ 。

（2）每件物品要么不带，要么只能整件携带。

这是决策问题中比较经典的 0-1 规划问题，要么带要么不带，是一个二值逻辑问题。

$\text{max}z=\sum\limits_{i=1}^{n}c_{i}x_{i}, \\ \text{s.t.}\left\{\begin{matrix} \sum\limits_{i=1}^{n}a_{i}x_{i} \leqslant b, \hfill \\ x_{i}=0 \ or \ 1,\ i=1,2,\cdots,n. \end{matrix} \right.$

例 4.7 指派问题

某单位有 $n$ 项任务，正好需要 $n$ 个人去完成，假设分配每个人只能完成一项任务。设 $c_{ij}$ 表示分配第 $i$ 个人去完成第 $j$ 项任务的费用（时间等），问应如何指派，完成任务的总费用最小？

建立 0-1 整数规划模型：

$\text{max}z=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n} c_{ij}x_{ij}, \\ \text{s.t.}\left\{\begin{matrix} \sum\limits_{j=1}^{n}x_{ij}=1, \ i=1,2,\cdots,n,\hfill \\ \sum\limits_{i=1}^{n}x_{ij}=1, \ j=1,2,\cdots,n,\hfill \\ x_{ij}=0 \ or \ 1,\ i,j=1,2,\cdots,n. \end{matrix} \right.$

例 4.8 旅行商问题（货郎担问题）

有一推销员，从城市 $v_{1}$ 出发，要遍历城市 $v_{2},v_{3},\cdots,v_{n}$ 各一次，最后返回 $v_{1}$ 。已知从 $v_{i}$ 到 $v_{j}$ 的旅费为 $c_{ij}$ ，试问应按怎样的次序访问这些城市，使得总旅费最少？

建立 0-1 整数规划模型：

$\text{max}z=\sum\limits_{i=1}^{n}\sum\limits_{j=1}^{n} c_{ij}x_{ij}, \\ \text{s.t.}\left\{\begin{matrix} \sum\limits_{i=1}^{n}x_{ij}=1, \ j=1,2,\cdots,n,\hfill \\ \sum\limits_{j=1}^{n}x_{ij}=1, \ i=1,2,\cdots,n,\hfill \\ u_{i}-u_{j}+nx_{ij} \leqslant n-1,\ i=1,\cdots,n,\ j=2,\cdots,n, \\ u_{1}=0,1 \leqslant u_{i} \leqslant n-1,\ i=2,3,\cdots,n, \hfill \\ x_{ij}=0 \ or \ 1,\ i,j=1,2,\cdots,n. \hfill \end{matrix} \right.$

4.2.2 整数线性规划模型的求解

例 4.9 为了生产需要，某工厂的一条生产线需要每天 24h 不间断运转，但是每天不同时段所需要的工人最低数量不同，具体数据如表 4.5 所示。已知每名工人的连续工作时间为 8h。则该工厂应该为生产线配备多少名工人，才能保证生产线的正常运转？

表 4.5 工人数量需求表
班次	1	2	3	4	5	6
时间段	0:00-4:00	4:00-8:00	8:00-12:00	12:00-16:00	16:00-20:00	20:00-24:00
工人数量	35	40	50	45	55	30

$\text{min}z=\sum\limits_{i=1}^{6}x_{i}, \\ \text{s.t.} \left \{ \begin{matrix} x_{1}+x_{6} \geqslant 35, \hfill \\ x_{1}+x_{2} \geqslant 40, \hfill \\ x_{2}+x_{3} \geqslant 50, \hfill \\ x_{3}+x_{4} \geqslant 45, \hfill \\ x_{4}+x_{5} \geqslant 55, \hfill \\ x_{5}+x_{6} \geqslant 30, \hfill \\ x_{i} \geqslant 0, \text{int},\ i=1,2,\cdots,6. \end{matrix} \right.$

# 程序文件 e4_9_1.py
import cvxpy as cp
x = cp.Variable(6, integer=True)
obj = cp.Minimize(sum(x))
cons = [x[0]+x[5]>=35,x[0]+x[1]>=40,
       x[1]+x[2]>=50,x[2]+x[3]>=45,
       x[3]+x[4]>=55,x[4]+x[5]>=30,
       x>=0]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：', x.value)

# 求余运算
# 程序文件 ex4_9_2.py
import cvxpy as cp
import numpy as np
a = np.array([35, 40, 50, 45, 55, 30])
x = cp.Variable(6, integer=True)
obj = cp.Minimize(sum(x))
cons = [x>=0]
for i in range(6):
    cons.append(x[(i-1)%6]+x[i]>=a[i])
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：', x.value)

例 4.10 某连锁超市经营企业为了扩大规模，新租用 5 个门店，经过装修后再营业。现有 4 家装饰公司分别对 5 个门店的装修费用进行报价，具体数据如表 4.6 所列。为保证这些质量，规定每个装修公司最多承担两个店面的装修任务。为节省装修费用，该企业该如何分配装修任务？

表 4.6 装修费用表
门店	1	2	3	4	5
$A$	15	13.8	12.5	11	14.3
$B$	14.5	14	13.2	10.5	15
$C$	13.8	13	12.8	11.3	14.6
$D$	14.7	13.6	13	11.6	14

建立 0-1 整数规划模型：

$\text{min}z=\sum\limits_{i=1}^{4}\sum\limits_{j=1}^{5}c_{ij}x_{ij}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{i=1}^{4}x_{ij}=1,\ j=1,2,\cdots,5, \hfill \\ \sum\limits_{j=1}^{5}x_{ij} \leqslant2, \ i=1,2,\cdots,4, \hfill \\ x_{ij}=0 \ or \ 1, \ i=1,2,\cdots,4,\ j=1,2,\cdots,5. \end{matrix} \right.$

# 程序文件 ex4_10.py
import cvxpy as cp
import numpy as np
c = np.loadtxt('data4_10.txt')
x = cp.Variable((4, 5), integer=True)           # 定义决策变量
obj = cp.Minimize(cp.sum(cp.multiply(c, x)))    # 构造目标函数
cons = [0<=x, x<=1, cp.sum(x, axis=0)==1,       # 构造约束条件
        cp.sum(x, axis=1)<=2]
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')                    # 求解问题
print('最优解为：\n', x.value)
print('最优值为：', prob.value)

例 4.11 已知 10 个商业网点的坐标如表 4.7 所列，现要在 10 个网点中选择适当位置设置供应站，要求供应站只能覆盖 10km 之内的网点，且每个供应站最多供应 5 个网点，如何设置才能使供应站的数目最小，并求最小供应站的个数。

表 4.7 商业网点 x 坐标和 y 坐标数据
$x$	9.4888	8.7928	11.5960	11.5643	5.6756	9.8497	9.1756	13.1385	15.4663	15.5464
$y$	5.6718	10.3868	3.9294	4.4325	9.9658	17.6632	6.1517	11.8569	8.8721	15.5868

建立 0-1 整数规划模型：

$\text{min}\sum\limits_{i=1}^{10}x_{i}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{i=1}^{10}y_{ij} \geqslant 1,\ j=1,2,\cdots,10, \hfill \\ d_{ij}y_{ij} \leqslant 1,\ i,j=1,2,\cdots,10, \hfill \\ \sum\limits_{j=1}^{10}y_{ij} \leqslant 5,\ i=1,2,\cdots,10, \hfill \\ x_{i} \geqslant y_{ij}, \ i,j=1,2,\cdots,10, \hfill \\ x_{i}=y_{ii}, \ i=1,2,\cdots,10, \hfill \\ x_{i},y_{ji}=0\ or\ 1,\ i,j=1,2,\cdots,10. \end{matrix}\right.$

# 程序文件 ex4_11.py
import cvxpy as cp
import numpy as np
a = np.loadtxt('data4_11.txt')
d = np.zeros((10, 10))
for i in range(10):
    for j in range(10):
        d[i, j] = np.linalg.norm(a[:, i]-a[:, j])
x = cp.Variable(10, integer=True)
y = cp.Variable((10, 10), integer=True)
obj = cp.Minimize(sum(x))
cons = [sum(y)>=1, cp.sum(y, axis=1)<=5,
        x>=0, x<=1, y>=0, y<=1]
for i in range(10):
    cons.append(x[i]==y[i, j])
    for j in range(10):
        cons.append(d[i, j]*y[i, j]<=10*x[i])
        cons.append(x[i]>=y[i, j])
prob = cp.Problem(obj, cons)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：\n', x.value)
print('----------\n', y.value)

4.3 投资的收益与风险

例 4.12 （选自 1998 年全国大学生数学建模竞赛 A 题）市场上有 $n$ 种资产（如股票、债券、......） $s_{i}\ \left(i=1,2,\cdots,n \right )$ 供投资者选择，某公司有数额为 $M$ 的一笔相当大的资金可用作一个时期的投资。公司财务分析人员对这 $n$ 种资产进行评估，估算出在这一时期内购买资产 $s_{i}$ 的平均收益率为 $r_{i}$ ，并预测出购买 $s_{i}$ 的风险损失率为 $q_{i}$ 。考虑到投资越分散，总的风险越小，公司确定，当用这笔资金购买若干种资产时，总体风险可用所投资的 $s_{i}$ 中最大的一个风险来度量。

购买 $s_{i}$ 要付交易费，费率为 $p_{i}$ ，并且当购买额不超过给定值 $u_{i}$ 时，交易费按购买 $u_{i}$ 计算（不买无须付费）。另外，假设同期银行存款利率是 $r_{0}\left(r_{0}=5 \% \right )$ ，且既无交易费又无风险。

已知 $n=4$ 时的相关数据如表 4.8 所列。

表 4.8 4 种资产的相关数据
$s_{i}$	$r_{i}\ / \%$	$q_{i}\ /\%$	$p_{i}\ /\%$	$u_{i}\ /$ 元
$s_{1}$	28	2.5	1	103
$s_{2}$	21	1.5	2	198
$s_{3}$	23	5.5	4.5	52
$s_{4}$	25	2.6	6.5	40

试给该公司设计一种投资组合方案，即用给定的资金 $M$ ，有选择地购买若干种资产或存银行生息，使净收益尽可能大，而总体风险尽可能小。

模型一：固定风险水平，优化收益

$\text{max} \sum\limits_{i=0}^{n} \left(r_{i}-p_{i} \right )x_{i}, \\ \text{s.t.}\left \{ \begin{matrix} \dfrac{q_{i}x_{i}}{M} \leqslant a, \ i=1,2,\cdots,n, \\ \sum\limits_{i=0}^{n} \left(1+p_{i} \right )x_{i}=M, \hfill \\ x_{i} \geqslant 0, \ i=0,1,\cdots,n. \hfill \end{matrix}\right.$

模型二：固定盈利水平，极小化风险

$\text{min} \left \{ \underset{1\leqslant i \leqslant n}{\text{max}} \left \{ q_{i}x_{i}\right \} \right \}, \\ \text{s.t.}\left \{ \begin{matrix} \sum\limits_{i=0}^{n} \left( r_{i}-p_{i} \right )x_{i} \geqslant kM, \hfill \\ \sum\limits_{i=0}^{n} \left(1+p_{i} \right )x_{i}=M, \hfill \\ x_{i} \geqslant 0, \ i=0,1,\cdots,n. \hfill \end{matrix}\right.$

模型三：两个目标函数加权求和

$\text{min} \ w\left \{ \underset{1 \leqslant i \leqslant n}{\text{max}} \left \{ q_{i}x_{i}\right \}\right \}-\left(1-w \right )\sum\limits_{i=0}^{n}\left(r_{i}-p_{i} \right )x_{i}, \\ \text{s.t.}\left \{ \begin{matrix} \sum\limits_{i=0}^{n} \left( 1+p_{i} \right )x_{i}=M, \hfill \\ x_{i} \geqslant 0, \ i=0,1,2,\cdots,n. \end{matrix} \right.$

模型一求解

# 程序文件 ex4_12_1.py
import cvxpy as cp 
import pylab as plt

b = plt.array([0.025, 0.015, 0.055, 0.026])
c = plt.array([0.05, 0.27, 0.19, 0.185, 0.185])
x = cp.Variable(5, pos=True)
aeq = plt.array([1, 1.01, 1.02, 1.045, 1.065])
obj = cp.Maximize(c @ x)
a = 0; aa = []; Q = []; X = []; M = 10000;
while a < 0.05:
    con = [aeq @ x == M, cp.multiply(b, x[1:]) <= a*M]
    prob = cp.Problem(obj, con)
    prob.solve(solver='GLPK_MI')
    aa.append(a)
    Q.append(prob.value)
    X.append(x.value)
    a = a+0.001
plt.rc('text', usetex=True)
plt.rc('font', size=15)
plt.plot(aa, Q, 'r*')
plt.xlabel('$a$')
plt.ylabel('$Q$', rotation=0)
plt.show()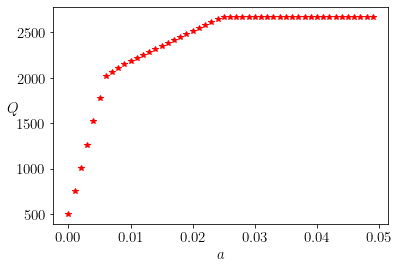

模型三求解

# 程序文件 ex4_12_2.py
import cvxpy as cp
import numpy as np
import pylab as plt

plt.rc('font', family='SimHei')
plt.rc('font', size=15)
x = cp.Variable(6, pos=True)
r = np.array([0.05, 0.28, 0.21, 0.23, 0.25])
p = np.array([0, 0.01, 0.02, 0.045, 0.065])
q = np.array([0, 0.025, 0.015, 0.055, 0.026])

def LP(w):
    V = []                # 风险初始化
    Q = []                # 收益初始化
    X = []                # 最优解的初始化
    con = [(1+p) @ x[:-1] == 10000, cp.multiply(q[1:], x[1:5]) <= x[5]]
    for i in range(len(w)):
        obj = cp.Minimize(w[i]*x[5]-(1-w[i])*((r-p) @ x[:-1]))
        prob = cp.Problem(obj, con)
        prob.solve(solver='GLPK_MI')
        xx = x.value      # 提出所有决策变量的取值
        V.append(max(q*xx[:-1]))
        Q.append((r-p) @ xx[:-1])
        X.append(xx)
    print('w=', w)
    print('V=', np.round(V, 2))
    print('Q=', np.round(Q, 2))
    plt.figure()
    plt.plot(V, Q, '*-')
    plt.grid('on')
    plt.xlabel('风险（元）')
    plt.ylabel('收益（元）')
    return X
    
w1 = np.arange(0, 1.1, 0.1)
LP(w1)
print('---------------')
w2 = np.array([0.766, 0.767, 0.810, 0.811, 0.824, 0.825, 0.962, 0.963, 1.0])
X = LP(w2)
print(X[-3])
plt.show()

4.4 比赛项目排序问题

例 4.13 （选自 2005 年电工杯数学建模竞赛 B 题）

在各种运动比赛中，为了使比赛公平、公正、合理地举行，一个基本要求是：在比赛项目排序过程中，尽可能使每个运动员不连续参加两项比赛，以便运动员恢复体力，发挥正常水平。

表 4.11 所列为某个小型运动会的比赛报名表。有 14 个比赛项目，40 名运动员参加比赛。表中第 1 行表示 14 个比赛项目，第 1 列表示 40 名运动员，表中 “#” 位置表示运动员参加此项比赛。建立此问题的数学模型，要求合理安排比赛项目顺序，使连续参加两项比赛的运动员人次尽可能地少。

表 4.11 某小型运动会的比赛报名表
	1	2	3	4	5	6	7	8	9	10	11	12	13	14
1		#	#						#				#
2								#			#	#
3		#		#						#
4			#					#				#
5											#		#	#
6					#	#
7												#	#
8										#				#
9		#		#						#	#
10	#	#		#			#
11		#		#									#	#
12								#		#
13					#					#				#
14			#	#				#
15			#					#				#
16									#		#	#
17						#								#
18							#					#
19			#							#
20	#		#
21									#					#
22		#			#
23							#					#
24							#	#					#	#
25	#	#								#
26					#									#
27						#					#
28		#						#
29	#										#	#
30				#	#
31						#		#				#
32							#			#
33				#		#
34	#		#										#	#
35				#	#							#
36				#			#
37	#								#	#
38						#		#		#				#
39					#			#	#				#
40						#	#		#				#

TSP 模型可表示为

$\text{min}z=\sum\limits_{i=1}^{15}\sum\limits_{j=1}^{15}w_{ij}x_{ij}, \\ \text{s.t.} \left \{ \begin{matrix} \sum\limits_{j=1}^{15}x_{ij}=1, \ i=1,2,\cdots,15, \hfill \\ \sum\limits_{i=1}^{15}x_{ij}=1, \ j=1,2,\cdots,15, \hfill \\ u_{i}-u_{j}+15x_{ij} \leqslant 14, \ i=1,2,\cdots,15,\ j=2,3,\cdots,15, \\ u_{1}=0, \ 1 \leqslant u_{i} \leqslant 14, \ i=2,3,\cdots,15, \hfill \\ x_{ij}=0 \ or \ 1, \ i,j=1,2,\cdots,15. \hfill \end{matrix} \right.$

# 程序文件 ex4_13.py
import numpy as np
import pandas as pd
import cvxpy as cp

a = pd.read_excel("data4_13_1.xlsx", header=None)
a = a.values
a[np.isnan(a)]=0                             # 把空格对应的不确定值替换为0
m,n = a.shape
w = np.ones((n+1, n+1))*10000000             # 邻接矩阵初始化
for i in range(n):
    for j in range(n):
        if i != j:
            w[i, j] = sum(a[:, i]*a[:, j])
for i in range(n):
    w[i, n] = 0
    w[n, i] = 0
wd = pd.DataFrame(w)
wd.to_excel('data4_13_2.xlsx')               # 把邻接矩阵保存到 Excel 文件
x = cp.Variable((n+1, n+1), integer=True)
u = cp.Variable(n+1, integer=True)
obj = cp.Minimize(cp.sum(cp.multiply(w, x)))
con = [cp.sum(x, axis=0) == 1, cp.sum(x, axis=1) == 1,
      x>=0, x<=1, u[0]==0, u[1:]>=1, u[1:]<=n]
for i in range(n+1):
    for j in range(1, n+1):
        con.append(u[i]-u[j]+(n+1)*x[i, j]<=n)
prob = cp.Problem(obj, con)
prob.solve(solver='GLPK_MI')
print('最优值为：', prob.value)
print('最优解为：\n', x.value)
i,j = np.nonzero(x.value)
print('xij=1对应的行列位置如下：')
print(i+1)
print(j+1)

最优值为： 2.0
最优解为：
 [[0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0.]
 [0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
 [0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0.]
 [0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]
 [0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 1. 0. 0. 0.]
 [0. 0. 0. 1. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0. 0.]]
xij=1对应的行列位置如下：
[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15]
[ 5 14  6  9 11  2  3  1  8 13  7 10 15 12  4]

TSP 回路为： $15\rightarrow 4\rightarrow 9\rightarrow 8\rightarrow 1\rightarrow 5\rightarrow 11\rightarrow 7\rightarrow 3\rightarrow 6\rightarrow 2\rightarrow 14\rightarrow 12\rightarrow 10\rightarrow 13\rightarrow 15$

本文链接：https://blog.csdn.net/dezon/article/details/133496778

原作者删帖不实内容删帖广告或垃圾文章投诉

智能推荐

使用nginx解决浏览器跨域问题_nginx不停的xhr-程序员宅基地

文章浏览阅读1k次。通过使用ajax方法跨域请求是浏览器所不允许的，浏览器出于安全考虑是禁止的。警告信息如下：不过jQuery对跨域问题也有解决方案，使用jsonp的方式解决，方法如下：$.ajax({ async:false, url: 'http://www.mysite.com/demo.do', // 跨域URL ty..._nginx不停的xhr

在 Oracle 中配置 extproc 以访问 ST_Geometry-程序员宅基地

文章浏览阅读2k次。关于在 Oracle 中配置 extproc 以访问 ST_Geometry，也就是我们所说的使用空间SQL 的方法，官方文档链接如下。http://desktop.arcgis.com/zh-cn/arcmap/latest/manage-data/gdbs-in-oracle/configure-oracle-extproc.htm其实简单总结一下，主要就分为以下几个步骤。..._extproc

Linux C++ gbk转为utf-8_linux c++ gbk->utf8-程序员宅基地

文章浏览阅读1.5w次。linux下没有上面的两个函数，需要使用函数 mbstowcs和wcstombsmbstowcs将多字节编码转换为宽字节编码wcstombs将宽字节编码转换为多字节编码这两个函数，转换过程中受到系统编码类型的影响，需要通过设置来设定转换前和转换后的编码类型。通过函数setlocale进行系统编码的设置。linux下输入命名locale -a查看系统支持的编码_linux c++ gbk->utf8

IMP-00009: 导出文件异常结束-程序员宅基地

文章浏览阅读750次。今天准备从生产库向测试库进行数据导入，结果在imp导入的时候遇到“ IMP-00009:导出文件异常结束” 错误，google一下，发现可能有如下原因导致imp的数据太大，没有写buffer和commit两个数据库字符集不同从低版本exp的dmp文件，向高版本imp导出的dmp文件出错传输dmp文件时，文件损坏解决办法：imp时指定..._imp-00009导出文件异常结束

python程序员需要深入掌握的技能_Python用数据说明程序员需要掌握的技能-程序员宅基地

文章浏览阅读143次。当下是一个大数据的时代，各个行业都离不开数据的支持。因此，网络爬虫就应运而生。网络爬虫当下最为火热的是Python，Python开发爬虫相对简单，而且功能库相当完善，力压众多开发语言。本次教程我们爬取前程无忧的招聘信息来分析Python程序员需要掌握那些编程技术。首先在谷歌浏览器打开前程无忧的首页，按F12打开浏览器的开发者工具。浏览器开发者工具是用于捕捉网站的请求信息，通过分析请求信息可以了解请..._初级python程序员能力要求

Spring @Service生成bean名称的规则（当类的名字是以两个或以上的大写字母开头的话，bean的名字会与类名保持一致）_@service beanname-程序员宅基地

文章浏览阅读7.6k次，点赞2次，收藏6次。@Service标注的bean，类名：ABDemoService查看源码后发现，原来是经过一个特殊处理：当类的名字是以两个或以上的大写字母开头的话，bean的名字会与类名保持一致public class AnnotationBeanNameGenerator implements BeanNameGenerator { private static final String C..._@service beanname

随便推点

二叉树的各种创建方法_二叉树的建立-程序员宅基地

文章浏览阅读6.9w次，点赞73次，收藏463次。1.前序创建#include<stdio.h>#include<string.h>#include<stdlib.h>#include<malloc.h>#include<iostream>#include<stack>#include<queue>using namespace std;typed_二叉树的建立

解决asp.net导出excel时中文文件名乱码_asp.net utf8 导出中文字符乱码-程序员宅基地

文章浏览阅读7.1k次。在Asp.net上使用Excel导出功能，如果文件名出现中文，便会以乱码视之。解决方法： fileName = HttpUtility.UrlEncode(fileName, System.Text.Encoding.UTF8);_asp.net utf8 导出中文字符乱码

笔记-编译原理-实验一-词法分析器设计_对pl/0作以下修改扩充。增加单词-程序员宅基地

文章浏览阅读2.1k次，点赞4次，收藏23次。第一次实验词法分析实验报告设计思想词法分析的主要任务是根据文法的词汇表以及对应约定的编码进行一定的识别，找出文件中所有的合法的单词，并给出一定的信息作为最后的结果，用于后续语法分析程序的使用；本实验针对 PL/0 语言的文法、词汇表编写一个词法分析程序，对于每个单词根据词汇表输出： (单词种类, 单词的值) 二元对。词汇表：种别编码单词符号助记符0beginb..._对pl/0作以下修改扩充。增加单词

android adb shell 权限,android adb shell权限被拒绝-程序员宅基地

文章浏览阅读773次。我在使用adb.exe时遇到了麻烦.我想使用与bash相同的adb.exe shell提示符,所以我决定更改默认的bash二进制文件(当然二进制文件是交叉编译的,一切都很完美)更改bash二进制文件遵循以下顺序> adb remount> adb push bash / system / bin /> adb shell> cd / system / bin> chm..._adb shell mv 权限

投影仪-相机标定_相机-投影仪标定-程序员宅基地

文章浏览阅读6.8k次，点赞12次，收藏125次。1. 单目相机标定引言相机标定已经研究多年，标定的算法可以分为基于摄影测量的标定和自标定。其中，应用最为广泛的还是张正友标定法。这是一种简单灵活、高鲁棒性、低成本的相机标定算法。仅需要一台相机和一块平面标定板构建相机标定系统，在标定过程中，相机拍摄多个角度下（至少两个角度，推荐10~20个角度）的标定板图像（相机和标定板都可以移动），即可对相机的内外参数进行标定。下面介绍张氏标定法（以下也这么称呼）的原理。原理相机模型和单应矩阵相机标定，就是对相机的内外参数进行计算的过程，从而得到物体到图像的投影_相机-投影仪标定

Wayland架构、渲染、硬件支持-程序员宅基地

文章浏览阅读2.2k次。文章目录Wayland 架构Wayland 渲染Wayland的硬件支持简述：　翻译一篇关于和 wayland 有关的技术文章, 其英文标题为Wayland Architecture .Wayland 架构若是想要更好的理解 Wayland 架构及其与 X (X11 or X Window System) 结构；一种很好的方法是将事件从输入设备就开始跟踪, 查看期间所有的屏幕上出现的变化。这就是我们现在对 X 的理解。内核是从一个输入设备中获取一个事件，并通过 evdev 输入_wayland