如何理解最小二乘法？-程序员宅基地

最小平方法是十九世纪统计学的主题曲。从许多方面来看, 它之于统计学就相当于十八世纪的微积分之于数学。
----乔治·斯蒂格勒的《The History of Statistics》

1 日用而不知

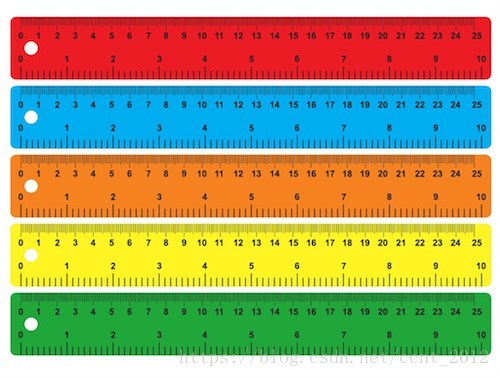
来看一个生活中的例子。比如说，有五把尺子：

用它们来分别测量一线段的长度，得到的数值分别为（颜色指不同的尺子）：

$\begin{array}{c|c} \qquad\qquad&\qquad长度\qquad\\\hline \color{red}红& 10.2 \\\hline \color{blue}蓝& 10.3 \\\hline \color{orange}橙&9.8\\\hline \color{Goldenrod}黄&9.9\\\hline \color{green}绿&9.8\\\end{array}$

之所以出现不同的值可能因为：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

总之就是有误差，这种情况下，一般取平均值来作为线段的长度：

$\overline{x}=\frac{10.2+10.3+9.8+9.9+9.8}{5}=10$

日常中就是这么使用的。可是作为很事'er的数学爱好者，自然要想下：

这样做有道理吗？
用调和平均数行不行？
用中位数行不行？
用几何平均数行不行？

2 最小二乘法

换一种思路来思考刚才的问题。

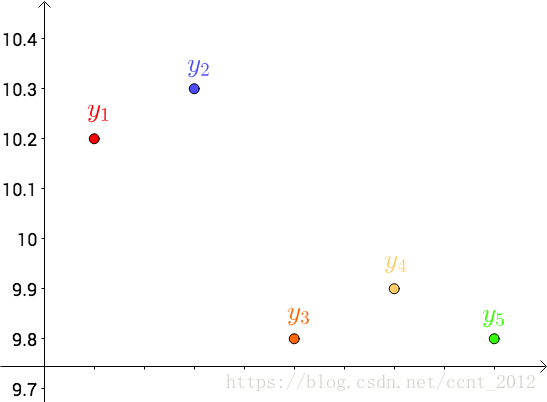
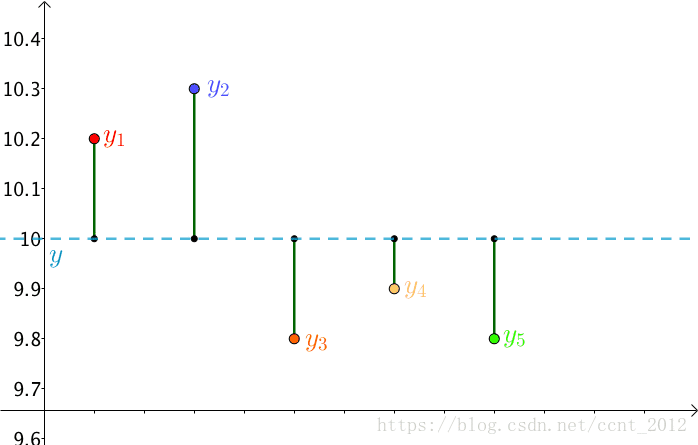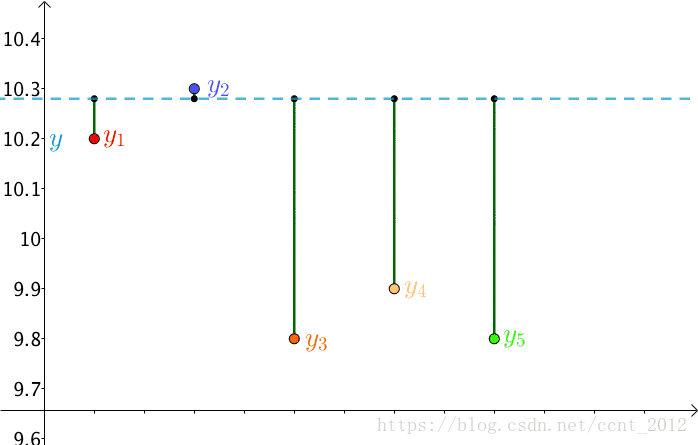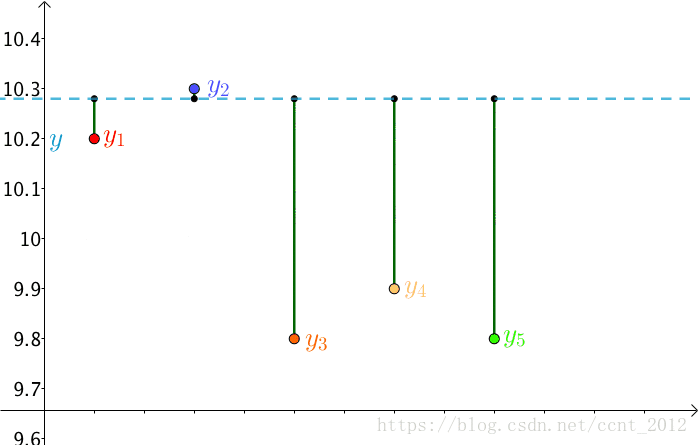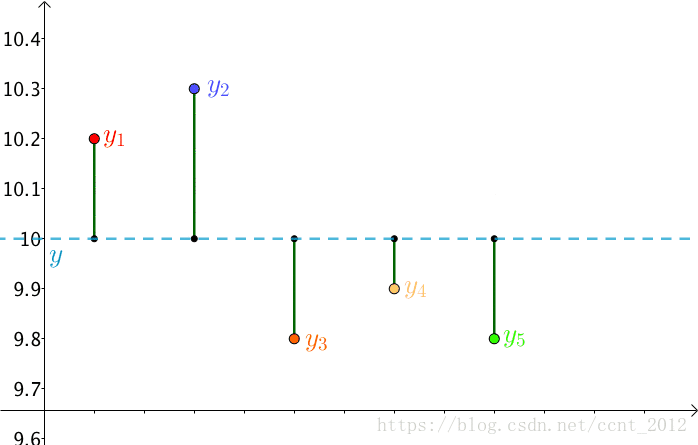
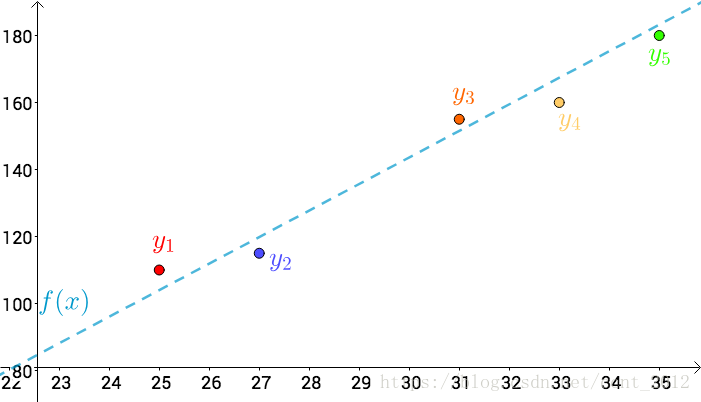
首先，把测试得到的值画在笛卡尔坐标系中，分别记作 $y_i$ ：

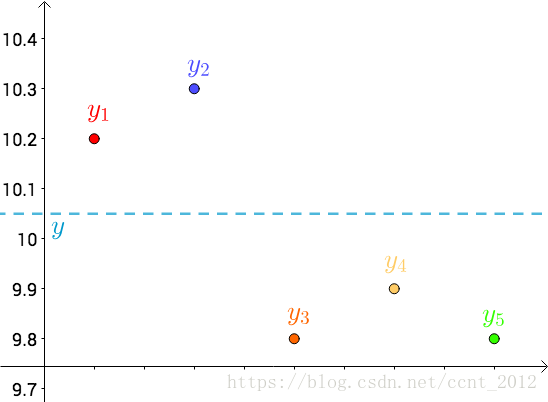
其次，把要猜测的线段长度的真实值用平行于横轴的直线来表示（因为是猜测的，所以用虚线来画），记作 $y$ ：

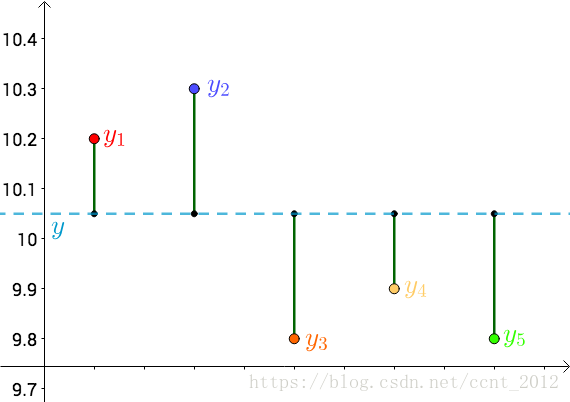
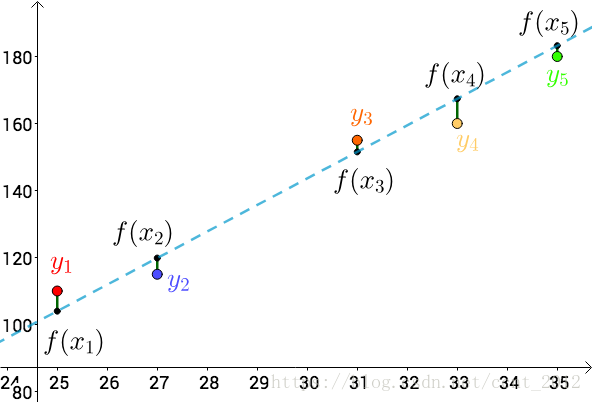
每个点都向 $y$ 做垂线，垂线的长度就是 $|y-y_i|$ ，也可以理解为测量值和真实值之间的误差：

因为误差是长度，还要取绝对值，计算起来麻烦，就干脆用平方来代表误差：

$|y-y_i|\to (y-y_i)^2$

总的误差的平方就是：

$\epsilon=\sum (y-y_i)^2$

因为 $y$ 是猜测的，所以可以不断变换：

自然，总的误差 $\epsilon$ 也是在不断变化的。

法国数学家，阿德里安-馬里·勒讓德（1752－1833，这个头像有点抽象）提出让总的误差的平方最小的 $y$ 就是真值，这是基于，如果误差是随机的，应该围绕真值上下波动（关于这点可以看下“如何理解无偏估计？”）。

这就是最小二乘法，即：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

这个猜想也蛮符合直觉的，来算一下。

这是一个二次函数，对其求导，导数为0的时候取得最小值：

$\begin{aligned} \frac{d}{dy}\epsilon &=\frac{d}{dy}\sum (y-y_i)^2=2\sum (y-y_i)\\ \quad\\ &=2((y-y_1)+(y-y_2)+(y-y_3)+(y-y_4)+(y-y_5))=0 \quad\\\end{aligned}$

进而：

$5y=y_1+y_2+y_3+y_4+y_5\implies y=\frac{y_1+y_2+y_3+y_4+y_5}{5}$

正好是算术平均数。

原来算术平均数可以让误差最小啊，这下看来选用它显得讲道理了。

以下这种方法：

$\epsilon=\sum (y-y_i)^2最小\implies 真值y$

就是最小二乘法，所谓“二乘”就是平方的意思，台湾直接翻译为最小平方法。

3 推广

算术平均数只是最小二乘法的特例，适用范围比较狭窄。而最小二乘法用途就广泛。

比如温度与冰淇淋的销量：

$\begin{array}{c|c} \qquad\qquad&\qquad销量\qquad\\\hline \color{red}{25^\circ}& 110 \\\hline \color{blue}{27^\circ}& 115 \\\hline \color{orange}{31^\circ}&155\\\hline \color{Goldenrod}{33^\circ}&160\\\hline \color{green}{35^\circ}&180\\\end{array}$

看上去像是某种线性关系：

可以假设这种线性关系为：

$f(x)=ax+b$

通过最小二乘法的思想：

上图的 $i,x,y$ 分别为：

$\begin{array}{c|c|c} \qquad i\qquad&\qquad x\qquad&\qquad y\qquad\\\hline 1&25& 110 \\\hline 2&27& 115 \\\hline 3&31&155\\\hline 4&33&160\\\hline 5&35&180\\\end{array}$

总误差的平方为：

$\epsilon=\sum (f(x_i)-y_i)^2=\sum (ax_i+b-y_i)^2$

不同的 $a,b$ 会导致不同的 $\epsilon$ ，根据多元微积分的知识，当：

$\begin{cases} \frac{\partial}{\partial a}\epsilon=2\sum (ax_i+b-y_i)x_i=0\\ \quad\\ \frac{\partial}{\partial b}\epsilon=2\sum (ax_i+b-y_i)=0\end{cases}$

这个时候 $\epsilon$ 取最小值。

对于 $a,b$ 而言，上述方程组为线性方程组，用之前的数据解出来：

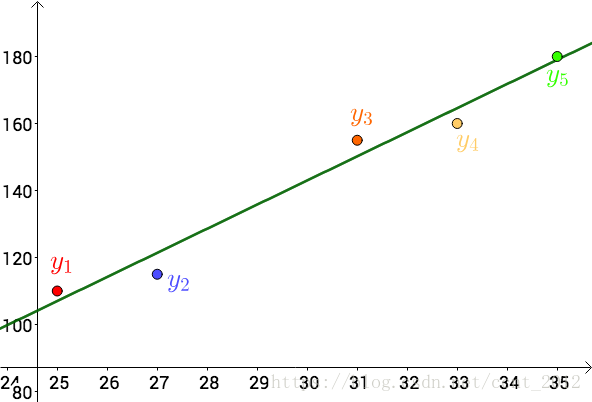
$\begin{cases} a\approx 7.2\\ \quad\\ b\approx -73\end{cases}$

也就是这根直线：

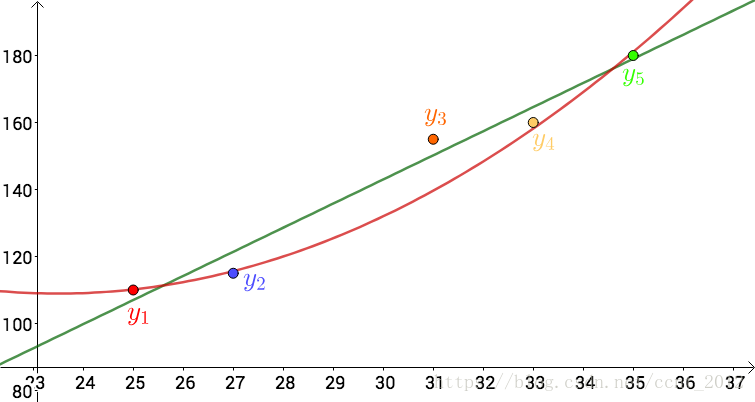
其实，还可以假设：

$f(x)=ax^2+bx+c$

在这个假设下，可以根据最小二乘法，算出 $a,b,c$ ，得到下面这根红色的二次曲线：

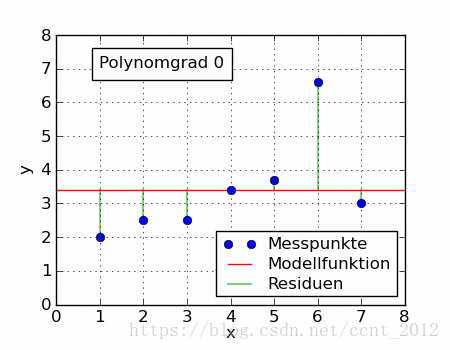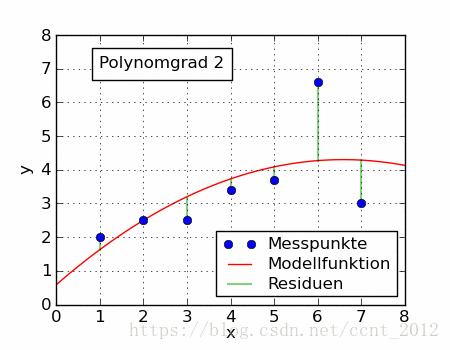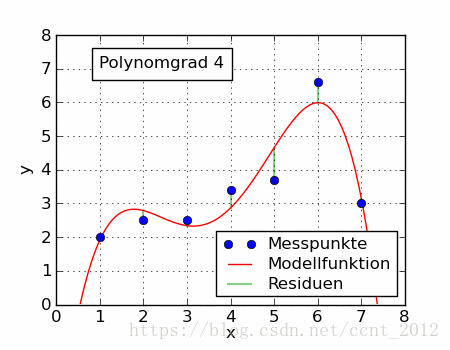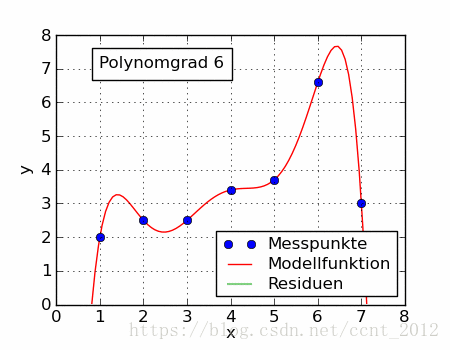
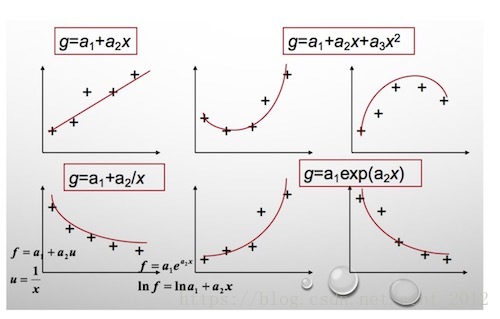
同一组数据，选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线（出处）：

不同的数据，更可以选择不同的 $f(x)$ ，通过最小二乘法可以得到不一样的拟合曲线：

$f(x)$ 也不能选择任意的函数，还是有一些讲究的，这里就不介绍了。

4 最小二乘法与正态分布

我们对勒让德的猜测，即最小二乘法，仍然抱有怀疑，万一这个猜测是错误的怎么办？

数学王子高斯（1777－1855）也像我们一样心存怀疑。

高斯换了一个思考框架，通过概率统计那一套来思考。

让我们回到最初测量线段长度的问题。高斯想，通过测量得到了这些值：

每次的测量值 $x_i$ 都和线段长度的真值 $x$ 之间存在一个误差：

$\epsilon_i=x-x_i$

这些误差最终会形成一个概率分布，只是现在不知道误差的概率分布是什么。假设概率密度函数为：

$p(\epsilon)$

再假设一个联合概率密度函数，这样方便把所有的测量数据利用起来：

$\begin{aligned} L(x) &=p(\epsilon_1)p(\epsilon_2)\cdots p(\epsilon_5)\\ \quad\\ &=p(x-x_i)p(x-x_2)\cdots p(x-x_5)\end{aligned}$

讲到这里，有些同学可能已经看出来了上面似然函数了（关于似然函数以及马上要讲到的极大似然估计，可以参考“如何理解极大似然估计法？”）。

因为 $L(x)$ 是关于 $x$ 的函数，并且也是一个概率密度函数（下面分布图形是随便画的）：

根据极大似然估计的思想，概率最大的最应该出现（既然都出现了，而我又不是“天选之才”，那么自然不会是发生了小概率事件），也就是应该取到下面这点：

当下面这个式子成立时，取得最大值：

$\frac{d}{dx}L(x)=0$

然后高斯想，最小二乘法给出的答案是：

$x=\overline{x}=\frac{x_1+x_2+x_3+x_4+x_5}{5}$

如果最小二乘法是对的，那么 $x=\overline{x}$ 时应该取得最大值，即：

$\frac{d}{dx}L(x)|_{x=\overline{x}}=0$

好，现在可以来解这个微分方程了。最终得到：

$p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

这是什么？这就是正态分布啊。

并且这还是一个充要条件：

$x=\overline{x}\iff p(\epsilon)={1 \over \sigma\sqrt{2\pi} }\,e^{- {{\epsilon^2 \over 2\sigma^2}}}$

也就是说，如果误差的分布是正态分布，那么最小二乘法得到的就是最有可能的值。

那么误差的分布是正态分布吗？

我们相信，误差是由于随机的、无数的、独立的、多个因素造成的，比如之前提到的：

不同厂家的尺子的生产精度不同
尺子材质不同，热胀冷缩不一样
测量的时候心情起伏不定
......

那么根据中心极限定理（参考“为什么正态分布如此常见？”），误差的分布就应该是正态分布。

因为高斯的努力，才真正奠定了最小二乘法的重要地位。

文章最新版本在（有可能会有后续更新）：如何理解最小二乘法？

本文链接：https://blog.csdn.net/ccnt_2012/article/details/81127117

原作者删帖不实内容删帖广告或垃圾文章投诉

智能推荐

Spring Boot 获取 bean 的 3 种方式！还有谁不会？，Java面试官_springboot2.7获取bean-程序员宅基地

文章浏览阅读1.2k次，点赞35次，收藏18次。AutowiredPostConstruct 注释用于在依赖关系注入完成之后需要执行的方法上，以执行任何初始化。此方法必须在将类放入服务之前调用。支持依赖关系注入的所有类都必须支持此注释。即使类没有请求注入任何资源，用 PostConstruct 注释的方法也必须被调用。只有一个方法可以用此注释进行注释。_springboot2.7获取bean

Logistic Regression Java程序_logisticregression java-程序员宅基地

文章浏览阅读2.1k次。理论介绍节点定义package logistic;public class Instance { public int label; public double[] x; public Instance(){} public Instance(int label,double[] x){ this.label = label; th_logisticregression java

linux文件误删除该如何恢复？，2024年最新Linux运维开发知识点-程序员宅基地

文章浏览阅读981次，点赞21次，收藏18次。本书是获得了很多读者好评的Linux经典畅销书**《Linux从入门到精通》的第2版**。下面我们来进行文件的恢复，执行下文中的lsof命令，在其返回结果中我们可以看到test-recovery.txt (deleted)被删除了，但是其存在一个进程tail使用它，tail进程的进程编号是1535。我们看到文件名为3的文件，就是我们刚刚“误删除”的文件，所以我们使用下面的cp命令把它恢复回去。命令进入该进程的文件目录下，1535是tail进程的进程id，这个文件目录里包含了若干该进程正在打开使用的文件。

流媒体协议之RTMP详解-程序员宅基地

文章浏览阅读10w+次，点赞12次，收藏72次。RTMP(Real Time Messaging Protocol)实时消息传输协议是Adobe公司提出得一种媒体流传输协议，其提供了一个双向得通道消息服务，意图在通信端之间传递带有时间信息得视频、音频和数据消息流，其通过对不同类型得消息分配不同得优先级，进而在网传能力限制下确定各种消息得传输次序。_rtmp

微型计算机2017年12月下,2017年12月计算机一级MSOffice考试习题(二)-程序员宅基地

文章浏览阅读64次。2017年12月的计算机等级考试将要来临!出国留学网为考生们整理了2017年12月计算机一级MSOffice考试习题，希望能帮到大家，想了解更多计算机等级考试消息，请关注我们，我们会第一时间更新。2017年12月计算机一级MSOffice考试习题(二)一、单选题1). 计算机最主要的工作特点是( )。A.存储程序与自动控制B.高速度与高精度C.可靠性与可用性D.有记忆能力正确答案：A答案解析：计算...

20210415web渗透学习之Mysqludf提权（二）（胃肠炎住院期间转）_the provided input file '/usr/share/metasploit-fra-程序员宅基地

文章浏览阅读356次。在学MYSQL的时候刚刚好看到了这个提权，很久之前用过别人现成的，但是一直时间没去细想，这次就自己复现学习下。 0x00 UDF 什么是UDF？ UDF (user defined function)，即用户自定义函数。是通过添加新函数，对MySQL的功能进行扩充，就像使..._the provided input file '/usr/share/metasploit-framework/data/exploits/mysql

随便推点

webService详细-程序员宅基地

文章浏览阅读3.1w次，点赞71次，收藏485次。webService一 WebService概述1.1 WebService是什么WebService是一种跨编程语言和跨操作系统平台的远程调用技术。Web service是一个平台独立的，低耦合的，自包含的、基于可编程的web的应用程序，可使用开放的XML（标准通用标记语言下的一个子集）标准...

Retrofit(2.0)入门小错误 -- Could not locate ResponseBody xxx Tried: * retrofit.BuiltInConverters_已添加addconverterfactory 但是 could not locate respons-程序员宅基地

文章浏览阅读1w次。前言照例给出官网：Retrofit官网其实大家学习的时候，完全可以按照官网Introduction，自己写一个例子来运行。但是百密一疏，官网可能忘记添加了一句非常重要的话，导致你可能出现如下错误：Could not locate ResponseBody converter错误信息：Caused by: java.lang.IllegalArgumentException: Could not l_已添加addconverterfactory 但是 could not locate responsebody converter

一套键鼠控制Windows+Linux——Synergy在Windows10和Ubuntu18.04共控的实践_linux 18.04 synergy-程序员宅基地

文章浏览阅读1k次。一套键鼠控制Windows+Linux——Synergy在Windows10和Ubuntu18.04共控的实践Synergy简介准备工作（重要）Windows服务端配置Ubuntu客户端配置配置开机启动Synergy简介Synergy能够通过IP地址实现一套键鼠对多系统、多终端进行控制，免去了对不同终端操作时频繁切换键鼠的麻烦，可跨平台使用，拥有Linux、MacOS、Windows多个版本。Synergy应用分服务端和客户端，服务端即主控端，Synergy会共享连接服务端的键鼠给客户端终端使用。本文_linux 18.04 synergy

nacos集成seata1.4.0注意事项_seata1.4.0 +nacos 集成-程序员宅基地

文章浏览阅读374次。写demo的时候遇到了很多问题，记录一下。安装nacos1.4.0配置mysql数据库，新建nacos_config数据库，并根据初始化脚本新建表，使配置从数据库读取，可单机模式启动也可以集群模式启动，启动时 ./start.sh -m standaloneapplication.properties 主要是db部分配置## Copyright 1999-2018 Alibaba Group Holding Ltd.## Licensed under the Apache License,_seata1.4.0 +nacos 集成

iperf3常用_iperf客户端指定ip地址-程序员宅基地

文章浏览阅读833次。iperf使用方法详解 iperf3是一款带宽测试工具，它支持调节各种参数，比如通信协议，数据包个数，发送持续时间，测试完会报告网络带宽，丢包率和其他参数。安装 sudo apt-get install iperf3 iPerf3常用的参数： -c ：指定客户端模式。例如：iperf3 -c 192.168.1.100。这将使用客户端模式连接到IP地址为192.16..._iperf客户端指定ip地址

浮点性(float)转化为字符串类型自定义实现和深入探讨C++内部实现方法_c++浮点数转字符串精度损失最小-程序员宅基地

文章浏览阅读7.4k次。写这个函数目的不是为了和C/C++库中的函数在性能和安全性上一比高低，只是为了给那些喜欢探讨函数内部实现的网友，提供一种从浮点性到字符串转换的一种途径。浮点数是有精度限制的，所以即使我们在使用C/C++中的sprintf或者cout 限制，当然这个精度限制是可以修改的。比方在C++中，我们可以cout.precision(10),不过这样设置的整个输出字符长度为10，而不是特定的小数点后1_c++浮点数转字符串精度损失最小